What is the Counterpart of Gaussian in a Hypergraph with respect to Graph?
In this article, I’d like to explore a counterpart of Gaussian in the hypergraph.
Note: This article is a promotion of our paper at AAAI2022.
Ever Wonder about an Extension from Pairwise Similarity to Multi-way Similarity?
We model a pairwise similarity of vector data using, say, a Gaussian. We use this similarity as a graph and apply a machine learning method. Do we have such a thing for hypergraph? In many papers on hypergraph algorithms, they tend to have a “cowboy modeling.” I want to shed some light on this area.
Hypergraph Modeling, why?
Using hypergraph modeling, we expect better results than graph modeling since hypergraphs take into account more effects. Particularly, if the vector data lies under some multi-way similarity, then we think that the hypergraph is a better fit than a graph. Consider the motion of the objects; we put sensors on the object, move the object around, and then we use the trajectory as data. Then, if we use three sensors, we can track the angles.
For researchers, we can think differently. You come up with a new hypergraph algorithm and want to try some real data. But do we have a nice way for the easy-try? Yeah, for a graph, you can easily construct a graph from a Gaussian kernel applied to a small dataset such as iris, wine, etc. Do we have such an easy way for hypergraph?
Gaussian Modeling for Graphs
Let’s start with a graph. Let $G := (V,E)$ be a graph, where $V := {1,\ldots,n}$ is a set of vertices, and $E$ is a set of edges. We represent a graph by a matrix $A \in \mathbb{R}^{n \times n}$ as \(A := a_{ij},\) where $a_{ij}$ is a weight of edge between the vertices $i$ and $j$. If there is no edge between $i$ and $j$, we assign 0. There are immensely many machine learning methods that work given a graph as an input.
The scenario today is that we are given vector data \(X = (\mathbf{x}_{1}, \ldots, \mathbf{x}_{n}),\quad \mathbf{x}_{i} \in \mathbb{R}^{d}.\)
Can we apply the graph machine learning method to this vector data? This seems to be a wild question because, by definition, graph machine learning methods require a graph as an input while we are given vector data as an input. In contrast to the wildness, this is frequently done. How? We now bring a kernel function $\kappa$, defined as \(\kappa(\mathbf{x}, \mathbf{y}) := \phi(\mathbf{x})^{\top} \phi(\mathbf{y}),\) where $\phi:\mathbb{R}^{d} \to \mathbb{R}^{d’} $ is called a feature map.
Using a kernel function $\kappa$, we construct a graph as \(A_{ij} = \kappa (\mathbf{x}_{i}, \mathbf{x}_{j}),\) and then apply a graph machine learning method to this graph. Typically, we choose a Gaussian kernel, that is defined as
\[\kappa (\mathbf{x}_{i}, \mathbf{x}_{j}) = \exp \left( -\gamma\|\mathbf{x}_{i} - \mathbf{x}_{j}\|_{2}^{2}\right).\]Hypergraph Modeling, how?
Let $H=(V,E)$ be a $2m$-uniform hypergraph, where $m \in \mathbb{N}$. A $2m$-uniform hypergraph is a generalized graph; each edge is allowed to connect $2m$ vertices. This hypergraph is represented by a tensor $\mathcal{A} \in \mathbb{R}^{\underbrace{n \times \ldots \times n}_{2m}}$
We here assume $2m$ data points
\[\mathbf{x}_{i_{1}},\ldots,\mathbf{x}_{i_{2m}} \in \mathbf{X}.\]I propose to formulate even $2m$ multi-way similarity function
\[\kappa^{(2m)}(\mathbf{x}_{i_{1}},\ldots,\mathbf{x}_{i_{2m}}) : \mathbf{X}^{m} \times\mathbf{X}^{m}\rightarrow\mathbb{R}\]as follows. I hereby define a kernel function $\kappa^{(2m)}$ which I shall call as biclique kernel as
\[\kappa^{(2m)} (\mathbf{x}_{i_{1}}, \ldots, \mathbf{x}_{2m}) := \sum_{\gamma=1}^{m}\sum_{\nu=m+1}^{2m} \kappa(\mathbf{x}_{i_{\gamma}},\mathbf{t}_{l_{\nu}} ),\]and propose to model a hypergraph as
\[\mathcal{A}_{i_{1}\ldots i_{2m}} := \kappa^{(2m)} (\mathbf{x}_{i_{1}}, \ldots, \mathbf{x}_{2m}).\]The example of the biclique kernel for biclique kernel for 4-uniform hypergraph is
\[\kappa^{(4)} (\mathbf{x}_{i_{1}}, \ldots, \mathbf{x}_{4}) = \kappa(\mathbf{x}_{1},\mathbf{x}_3)+\kappa(\mathbf{x}_{1},\mathbf{x}_4)+\kappa(\mathbf{x}_{2},\mathbf{x}_3) + \kappa(\mathbf{x}_{2},\mathbf{x}_4).\]If you use a Gaussian kernel, then
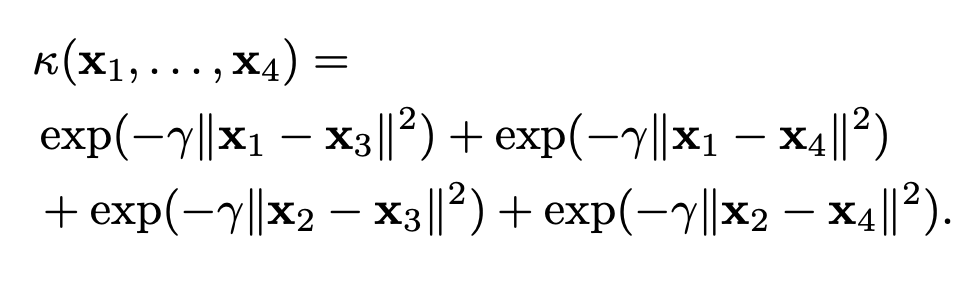
My proposal is that apply hypergraph machine learning methods to the hypergraph constructed by this biclique kernel.
Why this Modeling is Justified
Yes, I hear you. Why this is a good modeling. This modeling seems to be yet another “cowboy modeling.” Now, I’d like to give justifications for this modeling; why I can say that this is a good modeling in some sense.
To argue that, I first revisit why the heck the Gaussian kernel for a graph is justified. Then, I’ll show that this biclique kernel is a direct generalization of the graph justifications.
Hey, Wait, Why is Gaussian justified for a Graph?
Now, why is the Gaussian kernel a good modeling? Looking back at the graph case, we have several justifications for the Gaussian modeling.
First and foremost, the kernel function itself has rich theoretical foundations. Assume that we have $n$ data points $\mathbf{x}_{i} \in \mathbf{X}$.
Then, a gram matrix $K$ for a kernel function $\kappa$ which is defined as
\[K_{ij} := \kappa (\mathbf{x}_{i}, \mathbf{x}_{j}).\]Then, $K$ is a semi-definite. Also, if some matrix $K$ is semi-definite, then for $n$ data points we have a feature map that leads to $K$. This is one of the most foundational properties of kernel function, and we have richer theoretical properties and characteristics from this foundation.
One way to justify this is a heat kernel, by Belkin and Niyogi in the seminal paper. Consider a data point is randomly generated from a manifold $\mathbf{X}$, and we construct a graph by a Gaussian kernel as above. Then, in short, the graph Laplacian of this graph converges to the continuous Laplace operator defined over $\mathbf{X}$
Another way to justify this is the so-called spectral connection, which is established by Dhillon et al.. This connection provides a theoretical connection between spectral clustering and weighted kernel $k$-means. Spectral clustering is a very established clustering method for a graph; see the seminal tutorial paper for the details. Putting $\phi(\mathbf{x})$ to a weighted $k$-means framework, its $k$-means objective function is equivalent to the spectral clustering for a graph $A$, which is
\[A_{ij} := \phi(\mathbf{x}_{i})^{\top} \phi(\mathbf{x}_{j}).\]Justification for Biclique Kernel for Hypergraph
Now, we have an understanding of why the kernel function is justified. Let’s move on to hypergraph.
First, for the tensors, we have a similar notion of semi-definiteness.
A $m$-order tensor $\mathcal{A}$ is semidefinite if for any $\mathbf{x} \in \mathbb{R}^{n}$
\[\sum_{i_{1},\ldots, i_{m}} \mathcal{A}_{i_{1}\ldots i_{m}} x_{i_{1}} \ldots x_{i_{m}} \geq 0.\]Note that $m$ needs to be even since for odd $m$ this polynomial takes both of positive and negative values. For example of $m=3$, we have
\[\sum_{i_{1},i_{2}, i_{3}} \mathcal{A}_{i_{1}, i_{2}, i_{3}} (-x_{i_{1}}) (-x_{i_{2}}) (-x_{i_{3}}) = -\sum_{i_{1},i_{2}, i_{3}} \mathcal{A}_{i_{1}, i_{2}, i_{3}} x_{i_{1}} x_{i_{2}}x_{i_{3}},\]by which we observe that $\mathbf{x}$ and $-\mathbf{x}$ take different signs. This is why we model a hypergraph by an even-order uniform hypergraph.
For the tensors constructed from the biclique kernel, we can show that the tensor is semi-definite. The other direction also holds, i.e., if the tensor is semi-definite, then for a $n$ data points, there exists $\phi$ that satisfies the biclique kernel.
In my AAAI paper, we have a natural generalization of the heat kernel and spectral connection for hypergraph.
Yes, the biclique kernel has many supports, like a Gaussian kernel for the graph.
Conclusion
If you have once worked on hypergraph ML, you might have wondered how we can construct a hypergraph easily. Yes, the biclique kernel is there for you. With. Theories.
Citation:
If you find this piece useful, please cite our paper.
@inproceedings{saito2022hypergraph,
title={Hypergraph modeling via spectral embedding connection: Hypergraph cut, weighted kernel $k$-means, and heat kernel},
author={Saito, Shota},
booktitle={Proceedings of the AAAI Conference on Artificial Intelligence},
volume={36},
number={7},
pages={8141--8149},
year={2022}
}
